数値情報でない言語情報をもとに整理するためには、新QC七つ道具が適します。設計や企画などの場合には必ずしも数値データになるものばかりではありませんので、言語情報を扱えるツールとして新QC七つ道具が役に立ちます。
親和図法
混沌とした事象について、事実や発想などの親和性のある属性でまとめ構造化します。
何かの課題について要因を洗い出そうとブレーンストーミングを行っているときに、メンバーに要因となるものを言語情報としてポストイットなどに書き留めてもらって数多く挙げてもらったとします。これらの言語情報のなかから共通の属性をもつものをグループにして線で囲います。
こうすることで、混とんとしていた要因も整理することが出来きるようになります。
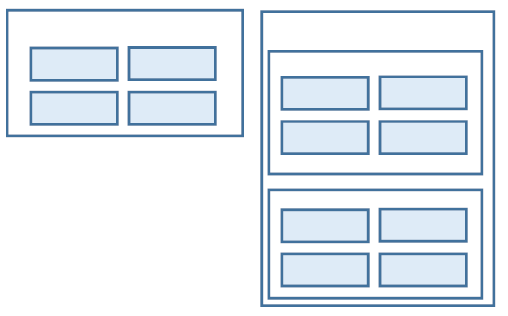
親和図法
連関図法
複雑に絡み合った原因と結果の関係をつないでいくことで、それぞれの関係を整理し明らかにします。QCストーリーの要因分析に連関図についてまとめていますので、そちらもご覧ください。
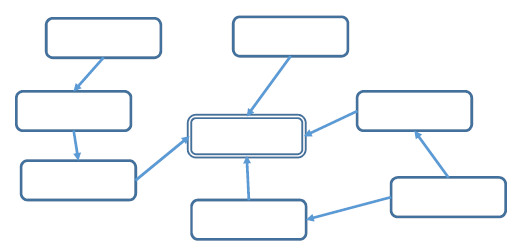
連関図

系統図法
目的に対する手段を繰り返し、必要な手段を明らかにします。QCストーリーの対策の立案に系統図についてまとめていますので、そちらもご覧ください。
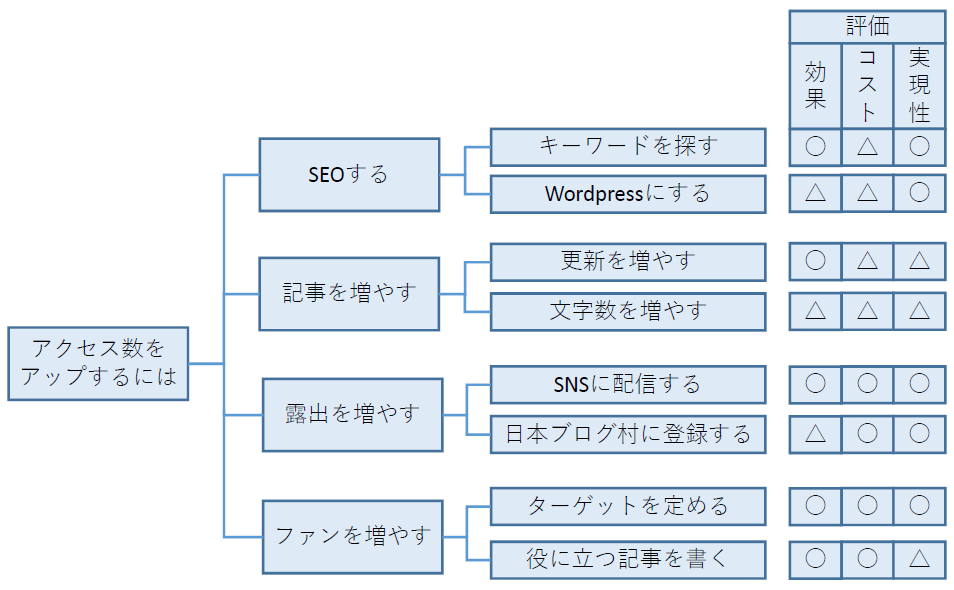
系統図

マトリックス図法
二つの要素間の関連性を評価し、問題点や改善点を探します。
それぞれの要素を色々な角度から評価してランク分けをします。例えば◎、〇、△、なしの四段階で評価を行ったり、◎は3点、〇は2点、△は1点のように点数をつけることで、それぞれの要素を比較したりします。
| 評価1 | 評価2 | 評価3 | 評価4 | |
|---|---|---|---|---|
| 要素A | ○ | △ | ○ | ◎ |
| 要素B | ○ | △ | ||
| 要素C | △ | ◎ | ||
| 要素D | ○ | △ | ○ | ○ |
アローダイアグラム法
複数の工程が関連しあう日程計画などで、最適な計画を立てることができます。
開発管理やプログラム管理を行う上で日程計画を立てる際にアローダイアグラム法が活用できます。日程計画を管理するのにガントチャートを用いることもありますが、ある作業が別の作業の成果物を要する場合など、その前後関係を明確にするためにはアローダイアグラム法のほうが明確にわかります。ですのでクリティカル・パスを考慮しながら日程短縮を検討する際に重宝します。
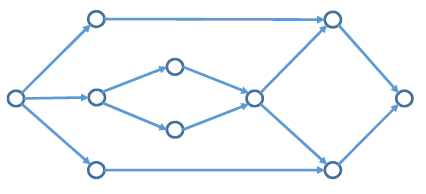
アローダイアグラム法
マトリックスデータ解析法
マトリックス法で定量化できる場合において、散布図で表し整理します。
新QC七つ道具は数値情報でない言語情報をもとに整理するのもですが、数値データを扱っているようにも見えます。しかし例えばアンケートで採点をお願いし、それぞれの人の主観に基づいた採点を様々な要素で行った場合などに傾向をつかむ目的でマトリックスデータ解析が使えます。
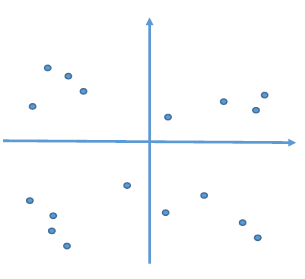
マトリックスデータ解析法
PDPC法
計画を完了するために、事前に様々な事態を想定して対応策も含めてそのプロセスを明らかにします。
起こるべき事態を書いておいて、それが起きたら行う方策をそれにつなげます。出発点とゴールがあって、その間に長方形に実施事項を入れて、楕円に想定される結果を書き矢印の線でつなげていきます。
不測の事態をひし形で表す場合がありますが、不測の事態も想定される結果の一つなのでひし形を使わなくても書くことが出来ます。
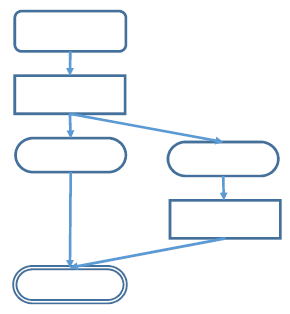
PDPC法






コメント